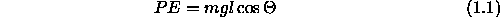
Often the most efficient way of finding the equations of motion for a robotic system is to apply the Euler-Lagrange equations. The first step involves computing the Lagrangian, which is the kinetic energy minus the potential energy of the system. The equations of motion are found by taking several partial derivatives of the Lagrangian and setting them equal to the applied forces (friction and motor torque).
Potential energy is stored in the inverted pendulum depending upon the elevation of the point mass m. (We make the assumption that the pendulum rod does not have any weight itself).
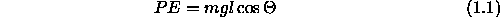
The kinetic energy of the rotating disk is
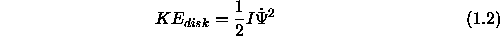
To calculate the total absolute kinetic enery of the point mass we must consider both the movement in horizontal as well as in vertical direction. The following figure clarifies the situation.
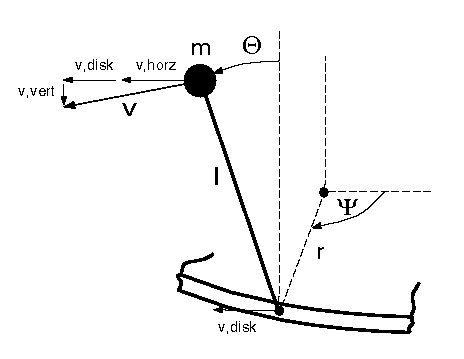
To the horizontal velocity componant of the point mass contributes also the rotation of the disk.
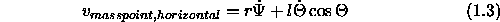
The vertical velocity component is
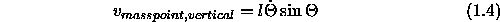
To gain the absolut value of velocity we sum up the squares of both velocity components.
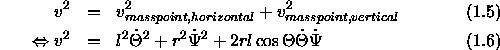
With eq. (1.6) the kinetic energy of the point mass is
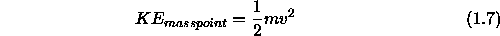
To write the Euler-Lagrange equations we will need to calculate a collection of partial derivatives of the Lagrangian L. Define L as
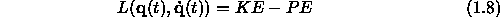
with
The vector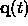 
contains the angular positions at the time "t" and the vector 
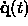the
angular velocities at the time "t" for the components of the inverted pendulum.
The dot over q is short hand for a derivative with respect to the time
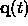"t". We will drop the explicit time dependence of and 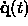from now on.
Note that L is a scalar expression.
The Euler-Lagrange equations are now defined as (vector notation)
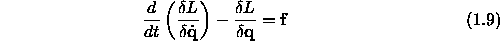
where the vector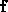 
consists of
the outer applied momentums, for example motor torque or friction. Viscous
friction (like found in a damper) is an example of nonconservative force.
Conservative forces can be integrated into the potential energy and do not need
to be included in 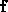. Eq. (1.9) is
just a different form of d'Alamberts Principle or the Newton Equation of motion.
We will not go more into the details of deriving the Euler-Lagrange Equations
here.
Let us now calculate the necessary derivatives to write out the Euler-Lagrange equations for our inverted pendulum. To do this, it is advisable to use vector and matrix notation instead of actually writing out the individual component relations. Inserting the terms for kinetic and potential energy in eq. (1.8) will yield to
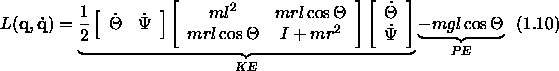
Eq. (1.10) can be written in short notation as
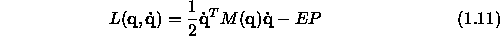
with the matrix M called the generalized mass matrix.
Let us consider the derivatives of the Lagrangian. For M symmetric we can write
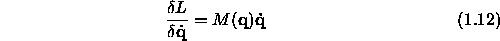
Using the product rule
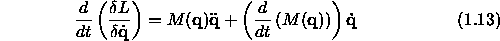
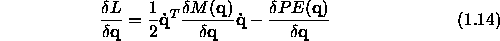
Notice that
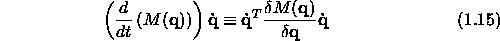
Now we can write down the Euler-Lagrange equation
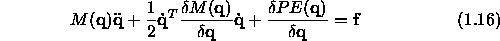
The physical meaning of the elements of the above eq. is as follows
It is - as you will see later - useful to solve the equation of motion for
the highest derivative which is in our case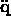 
, so that eq.
(1.16) takes the form
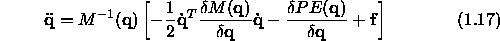
Equivilant to eq (1.17) is
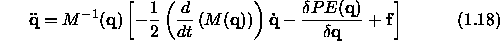
Note that the matrix M is invertable. (An n x n matrix is invertable if the determinant of the matrix is nonzero).
This has been quite formal up to now. Let's get somewhat more specific and write out eq. (1.18) by showing the contents of the involved matrices and vectors.
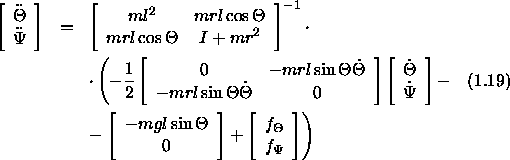
We want to have eq. (1.19) in the form
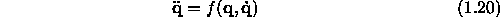
That's why we use a different notation as follows
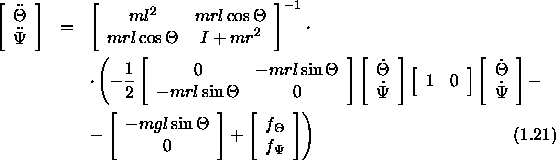
We have almost succeded now. One last step is to convert the above set of differential equations of second order into a set of differential equations of first order.
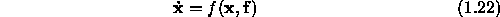
The resulting matrix notation for our system is a so called state representation ( see also book 'Introduction to Control Systems' from Dk Anand and later in this exercise ).
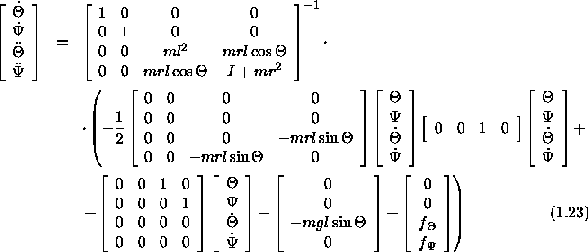
Let's write the above equation in shorter notation as
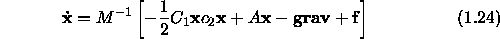
That sums up the tutorial on the Lagrange method. Now you are ready to implement these equations on the computer. Go back to the main exercise page.